Macht die Natur doch Sprünge? – Gedanken zur Chaostheorie
Natura non facit saltus(1) – “Die Natur macht keine Sprünge”, so heißt die Übersetzung des Satzes von Aristoteles im neueren Sprachgebrauch. Macht sie nicht vielleicht doch Sprünge?
2008 war der Begründer der Chaos-Theorie, der Meteorologe Edward Lorenz mit 90 Jahren gestorben. Lorenz forschte am MIT/ Massachusetts Institute of Technology (Boston) über Vorgänge, die den aristotelischen Satz relalitivieren.
Was beweist die Chaos-Theorie?
Sie beweist, dass auch manche Naturwissenschaftler in eingefahrenen Bahnen nach dem Schwarz-Weiß-Muster denken: entweder ein Naturgesetz gilt oder es gilt nicht!
Die meisten, welche die Theorie von E. Lorenz, die in Europa zu Beginn der 80-er Jahre durch spektakuläre Artikel in allen Zeitungen und Fernsehsendungen verfolgten, waren beeindruckt – merkwürdigerweise: ich nicht! Und zwar nicht deswegen, weil mich die Versuche und Überlegungen von Lorenz nicht beeindruckt hätten, sondern weil es mir schon damals, als ich zum ersten Mal davon hörte, völlig klar war, dass dies eine Bestätigung dessen ist, was für einen Naturwissenschaftler selbstverständlich sein sollte: Naturgesetze von denen wir (von der Schule her) gewohnt waren, sie durch hübsch verpackte Formeln als gegeben hinzunehmen, gelten immer nur für einen Teilbereich – also innerhalb gewisser Grenzen, die einen Anfang und ein Ende haben. Ganz selbstverständliche Regeln gelten plötzlich ab einem ganz bestimmten Punkt nicht mehr – danach gelten neue Regeln, die wieder nur bis zu einer gewissen Grenze gültig sind. Was mich an der Aufregung bei der Berichterstattung damals und heute noch stört, ist der „Chaosbegriff“ im Zusammenhang mit E. Lorenz, denn Lorenz fand ja nicht heraus, dass an einem Punkt das Chaos (was immer frau/man auch darunter verstehen mag) beginnt, sondern, dass neue Regeln gelten. So sehr ich den griechischen Philosophen und Wissenschaftler Aristoteles verehre, an einem seiner Sätze hatte ich stets etwas gezweifelt: „Die Natur macht keine Sprünge“ – Die Natur macht durchaus Sprünge, wie das nicht zuletzt von Max Planck durch die Quantentheorie bewiesen wurde, die mit ihren Aussagen die Newton’sche klassische Mechanik verdrängte (nicht ersetzte – denn in einem bestimmten Bereich gilt diese Mechanik ja auch heute noch). Ein weiterer Beweis war die oben genannte Chaos-Theorie.
Anm.: Aristoteles hatte allerdings seinen berühmten Satz vermutlich nicht auf die Naturwissenschaften, sondern auf den Gegenstand dieser Wissenschaften - die Natur selbst, bezogen.
Was besagt die Chaos-Theorie?
Kleinste Ursachen können ungeahnte, überraschende Folgen haben. Berühmt war der Ausspruch von Lorenz:
„Der Flügelschlag eines Schmetterlings im Amazonas-Urwald kann einen Orkan in Europa auslösen.“
Es soll hier nicht tiefer in die Chaostheorie eingedrungen werden, wer sich dafür interessiert, findet durch eine google-Suche alles was frau/man als interessierter Mensch zu diesem Thema wissen sollte. Es sollen hier nur zwei typische Beispiele erwähnt werden:
1. Wenn man ein Auto in einen Windkanal stellt und an die Oberfläche des Autos bewegliche Fasern anbringt, die igelartig von der Oberfläche abstehen, so werden sich diese Fasern bei Beginn der Windzufuhr zunächst leicht in Windrichtung neigen, steigert man die Windgeschwindigkeit, so neigen sich die Fasern weiter und zwar immer stärker je mehr die Windgeschwindigkeit gesteigert wird – und dann kommt plötzlich der Punkt, an welchem bei einer weiteren Steigerung der Windgeschwindigkeit die Fasern sich nicht mehr nach einer zur Windgeschwindigkeit linearen Relation weiter in Windrichtung biegen, sondern wild zu flattern anfangen. Dies ist also jener von Lorenz beobachtete Punkt, ab dem geltende Gesetze schlagartig nicht mehr gelten.
2. Wenn man in einen Fischteich etwas mehr Futter einbringt, so werden in absehbarer Zeit (vielleicht im nächsten Jahr) mehr Fische im Teich schwimmen, bei weiterer Futterzufuhr erhöht sich die Anzahl der Fische – bis an einem bestimmten Punkt ein eigenartiges Phänomen auftritt: es gibt plötzlich nur noch sehr wenige Fische. Im nächsten Jahr kann dann u.U. eine gewaltige Fischmenge beobachtet werden, die im übernächsten Jahr wieder stark abnimmt und in den Folgejahren großen Schwankungen unterworfen ist. Die Relation „je mehr Futter, desto mehr Fische“ stimmt plötzlich nicht mehr.
Wie wir heute durch die Chaostheorie wissen, lassen sich solche Effekte nach neuen, etwas komplizierteren mathematischen Formeln sehr wohl berechnen.
In den folgenden Jahren wurde versucht, die komplizierten mathematischen Regeln, die aus der Chaostheorie resultierten, auf nahezu alle komplexe Vorgänge anzuwenden: Wetter, Wirtschaftskreisläufe (insbesondere Börsenprognosen) und neuronale Netze.
Es gibt viele wertvolle Ergebnisse der Chaosforschung – in der Prognose von Börsenverläufen gibt es z.B. komplizierte Vorhersagemodelle. Leider ist die mathematisch nachvollziehbare Börsenprognose des Börsencrashs von 1987 erst 10 Jahre später, also im „Nachhinein“ entwickelt worden und hat sich auch bis heute nicht als geeignet erwiesen, künftige Crashs vorherzusagen. Schade – oder „Gott sei Dank“!
(1) Der Satz von Aristoteles wurde von vielen Wissenschaftlern bis hin in die Neuzeit immer wieder neu formuliert (auch: „natura non saltum facit“, u. a. als Axiom von Carl von Linné (1707-1778)
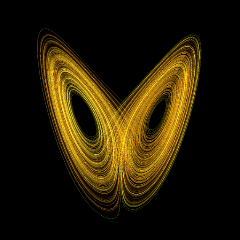
(2) Lorenz-Attraktor in einem dreidimensionalen Phasenraum, dem ein einfaches Wettermodell zugrunde liegt. Der Bahnpunkt kreist links im Uhrzeigersinn und rechts entgegen. Bei jedem Umlauf verbreitert sich das Band der Bahnen auf das Doppelte und wird anschließend bei der Abwärtsbewegung in der Bildmitte in zwei Hälften zerschnitten, wobei die Entscheidung fällt, ob der nächste Umlauf links oder rechts stattfindet. Auf diesem Mechanismus beruht der chaotische Charakter der Bahnen (Zitat aus Wikipedia).
(2011)